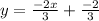1 Answer

Nefski · Answer 1 · 2020-04-24T15:44:51+0000

Equation of line passing through (2, -2) and parallel to 2x+3y = -8 is
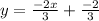
y=(-2 x)/(3)+(-2)/(3)

Need to write equation of line parallel to 2x+3y=-8 and passes through the point (2, -2)

Generic slope intercept form of a line is given by y = mx + c

where "m" = slope of the line and "c" is the y - intercept

Let’s first find slope intercept form of 2x+3y=-8 to get slope of line

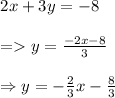
$\begin{array}{l}{2 x+3 y=-8} \\\\ {=>y=(-2 x-8)/(3)} \\\\ {\Rightarrow y=-(2)/(3) x-(8)/(3)}\end{array}$

On comparing above slope intercept form of given equation with generic slope intercept form y = mx + c,

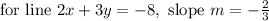
$\text {for line } 2 x+3 y=-8, \text { slope } m=-(2)/(3)$

We know that slopes of parallel lines are always equal

So the slope of line passing through (2, -2) is also
m=-(2)/(3)

Equation of line passing through
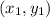(x_1 , y_1) and having slope of m is given by

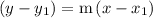
$\left(y-y_(1)\right)=\mathrm{m}\left(x-x_(1)\right)$

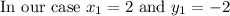
$\text { In our case } x_(1)=2 \text { and } y_(1)=-2$

Substituting the values in equation of line we get

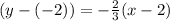
(y-(-2))=-(2)/(3)(x-2)

$\begin{array}{l}{\Rightarrow y+2=(-2 x+4)/(3)} \\\\ {=>3(y+2)=-2 x+4} \\\\ {=>3 y+6=-2 x+4} \\\\ {3 y=-2 x-2}\end{array}$

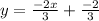
y=(-2 x)/(3)+(-2)/(3)

Hence equation of line passing through (2 , -2) and parallel to 2x + 3y = -8 is given as
y=(-2 x)/(3)+(-2)/(3)

Please log in or register to add a comment.