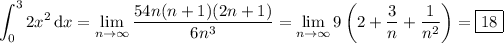We divide [0, 3] into
 subintervals,
subintervals,
![\left[0,\frac3n\right]\cup\left[\frac3n,\frac6n\right]\cup\left[\frac6n,\frac9n\right]\cup\cdots\cup\left[\frac{3(n-1)}n,3\right]](https://img.qammunity.org/2020/formulas/mathematics/college/va2mbhif6m12bjn9no9ryunewt8j629c3m.png)
so that the right endpoint of each subinterval is given according to the arithmetic sequence,
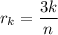
for
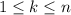 .
.
The Riemann sum is then
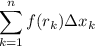
where

With
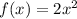 , we have
, we have
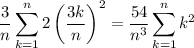
Recall that

The area under the curve
 over the interval [0, 3] is then
over the interval [0, 3] is then