Question

A right triangle is shown below whose sides are 2x, x2 - 1, and x2 + 1.

(a)
Prove the identity (2x)2 + (x2 - 1)2 = (x2 + 1)2
for x > 1.
x2 +1
.12-1​

Answer 1

`(2x)^2 + (x^2 - 1)^2 = (x^2 + 1)^2` PROVED

Explanation:

The sides of the given right triangle are :
`2x , (x^2 -1) , (x^2 +1)`

Now here, To show:
`(2x)^2 + (x^2 - 1)^2 = (x^2 + 1)^2` .... (1)

Now, by ALGEBRAIC IDENTITY:
`(a \pm b)^2  = a ^2 +b^2 \pm 2ab`

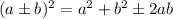
So here, similarly

`(x^2-1)^2 = (x^2)^2 + (1)^2 - 2 (x^2)\\(x^2+1)^2 = (x^2)^2 + (1)^2+ 2 (x^2)`

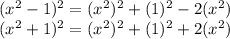
Now, substituting the value on Left side of (1) , we get :

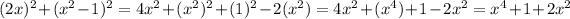`(2x)^2 + (x^2 - 1)^2   = 4x^2 + (x^2)^2 + (1)^2 - 2 (x^2) = 4x^2 + (x^4) + 1 - 2 x^2  = x^4 + 1 + 2x^2` ...... (a)

Also, the right side of (1) is:

`(x^2 + 1)^2 = (x^2)^2 + (1)^2+ 2 (x^2)  = x^4 + 1 + 2x^2` ... (b)

from(a) and (b) we see that

`x^4 + 1 + 2x^2 = x^4 + 1 + 2x^2\\\implies(2x)^2 + (x^2 - 1)^2 = (x^2 + 1)^2`

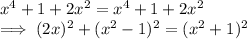
HENCE PROVED.