Answer:
The values of 'x' are -1.2, 0, 0,
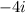 or
or
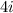 .
.
Explanation:
Given:
The equation to solve is given as:
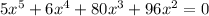
Factoring
 from all the terms, we get:
from all the terms, we get:
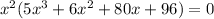
Now, rearranging the terms, we get:
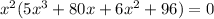
Now, factoring
 from the first two terms and 6 from the last two terms, we get:
from the first two terms and 6 from the last two terms, we get:
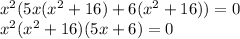
Now, equating each factor to 0 and solving for 'x', we get:
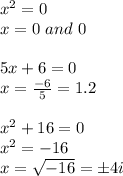
There are 3 real values and 2 imaginary values. The value of 'x' as 0 is repeated twice.
Therefore, the values of 'x' are -1.2, 0, 0,
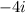 or
or
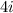 .
.