Question

Given that point S is equidistant from the sides of triangle WXY, find the following measures.

SU - 5, 12, 13, or 18
M m

Answer 1

Explanation:

5, 39, 24 just finished it

Answer 2

`SU=5\\\angle WXY = 24\°\\\angle SYW = 39 \°`

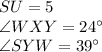
Explanation:

According to the graph,

`\angle WXT \cong \angle YXT`

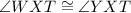
So,
`m\angle YXT =12 \°`

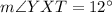
By sum of angles we have

`\angle WXY = \angle WXT + \angle YXT\\\angle WXY = 12 \° + 12\° = 24 \°\\\therefore \angle WXY 24\°`

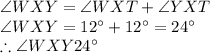
By given, we know that

`\angle UYS \cong \angle SYW\\\therefore \angle SYW = 39 \°`

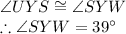
By given, we know that side SU is a leg of the right triangle SUX, where the hypotenuse is 13 units, and the opposite angle is 12°. However, if you look closer, you would find that side ST is 5 units, and by GIven we know that ST = SU.

Therefore, SU = 5.