Question

An online furniture store sells chairs for $50 each and tables for $250 each. Every day, the store can ship no more than 36 pieces of furniture and must sell at least $3400 worth of chairs and tables. If 23 chairs were sold, determine all possible values for the number of tables that the store must sell in order to meet the requirements. Your answer should be a comma separated list of values. If there are no possible solutions , submit an empty answer.

Answer 1

9,10,11,12,13

Explanation:

cuz

Answer 2

All possible values for the number of tables that the store must sell in order to meet the requirements are 9, 10, 11, 12, 13.

Explanation:

Let x be the number of chairs sold and y be the number of tables sold.

Chairs are sold for $50 each, then x chairs cost $50x.

Tables are sold for $250 each, then y tables cost $250y.

In total, x chairs and y tables cost $(50x+250y).

Every day, the store can ship no more than 36 pieces, then

`x+y\le 36`

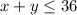
Every day, the store must sell at least $3,400 worth of chairs and tables, then

`50x+250y\ge 3,400`

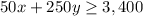
If 23 chairs were sold, then x = 23. Substitute it into the inequalities:

`23+y\le 36\Rightarrow y\le 13\\ \\50\cdot 23+250y\ge 3,400\Rightarrow 250y \ge 2,250,\ \ \ y\ge 9`

Thus
`9\le y\le 13`

This means all possible values for the number of tables that the store must sell in order to meet the requirements are 9, 10, 11, 12, 13.