Answer:
The measure of side BD is 8.6 and The measure of side CE is 8.4
Explanation:
Given as :
The Triangle is ABC with side AB , BC , CA
And The points E and D is on the side AB and AC
So, AED is a Triangle
And Δ AED
 Δ ABC
Δ ABC
The measure of side AD = 6.9
The measure of side AE = 7.2
The measure of side ED = 5.2
The measure of side BC = 10.2
Let The The measure of side EB = x
And The measure of side DC = y
So, From similarity property
 =
=
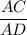 =
=
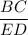
Or,
 =
=
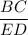
So,
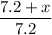 =
=
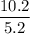
Or, 5.2 × ( 7.2 + x ) = 10.2 × 7.2
Or, 37.44 + 5.2 x = 73.44
Or, 73.44 - 37.44 = 5.2 x
∴ x =
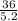
I.e x = 6.9
Now in Δ BED
BE² + ED² = BD²
Or, 6.9² + 5.2² = BD²
Or, BD² = 74.65
∴ BD =
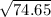
I.e BD = 8.64
Or, BD = 8.6
Similarly for y
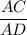 =
=
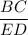
Or,
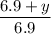 =
=
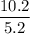
Or, 5.2 × ( 6.9 + y ) = 10.2 × 6.9
Or, 35.88 + 5.2 y = 70.38
or, 5.2 y = 70.8 - 35.88
Or, 5.2 y = 34.5
∴ y =
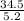
I.e y = 6.6
Now in Δ CED
CD² + ED² = CE²
Or, 6.6² + 5.2² = CE²
Or, CE² = 70.6
∴ CE =

I.e CE = 8.40
Or, CE = 8.4
Hence The measure of side BD is 8.6 and The measure of side CE is 8.4 Answer