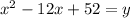Answer:
Explanation:
Describing the function rule means that you are going to write the equation of the parabola using that roots. If x = 6 + 4i, then the factor for that is
(x - 6 - 4i).
If x = 6 - 4i, then the factor for that is
(x - 6 + 4i).
FOILing that together gives you a long string of x- and i-terms with a constant or 2 thrown in:
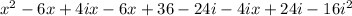
What's nice here is that 4ix and -4ix cancel each other out; likewise 24i and -24i. Once that is all canceled away, we are left with
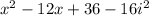
The i-squared is what makes this complex. i-squared = -1, so
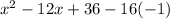 and
and
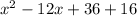 and
and