Question

Use sigma notation to represent the sum of the first six terms of the following sequence: −10, −13, −16, …

Answer 1

Sigma notation of sequence −10, −13, −16, … is
`\sum_(n=1)^(6)-(3 n+7)`

Solution:

Need to determine the sigma notation for the following sequence

−10, −13, −16, …

Let's try to build a generic formula for given sequence

The given sequence is in Arithmetic progression where first term = -10 and common difference = -3

The formula for arithmetic progression is given as:

`a_n = a_1 + (n - 1)d`

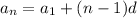
Where,

`a_n` is the nth term in the sequence

`a_1` is the first term in the sequence

d is the common difference between the terms

Here in this sequence
`a_1` = -10 and d = -3

`a_n = -10 + (n - 1)(-3)\\\\a_n = -10 - 3n + 3\\\\a_n = -3n - 7`

So generic formula for a term is – ( 3n + 7 )

`\begin{array}{l}{\text { For } \mathrm{n}=1, \text { term is }-(3 * 1+7)=-10} \\\\ {\text { For } \mathrm{n}=2, \text { term is }-(3 * 2+7)=-13} \\\\ {\text { For } \mathrm{n}=3, \text { term is }-(3 * 3+7)=-16}\end{array}`

And so on

Using sigma notation for arithmetic sequence:

`\sum_(k=1)^(n) a_(k)`

So for first six terms value of n will vary from 1 to 6 and in sigma notation it can be represented as

`\sum_(n=1)^(6)-(3 n+7)`