Question

If x=3t-8 and y=4+t, what equation expresses y in terms of x?

Answer 1

If x = 3t - 8 and y = 4 + t , then the equation
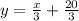`y=(x)/(3)+(20)/(3)` represents variable y in terms of x.

Solution:

Given two equations are

x = 3t - 8 ------(1)

y = 4 + t ------(2)

Need to determine the equation which express y in terms of x.

If we observer the two equations, common variable between the two is variable t.

So let’s first get the value of t in terms of x from equation 1.

`\begin{array}{l}{x=3 t-8} \\\\ {=>-3 t=-8-x} \\\\ {=>t=(-8-x)/(-3)=(x+8)/(3)} \\\\ {=>t=(x+8)/(3)}\end{array}`

`\text {On substituting } t=(x+8)/(3) \text { in equation }(2), \text { we get }`

`\begin{array}{l}{y=4+(x+8)/(3)} \\\\ {=>y=(12+x+8)/(3)} \\\\ {=>y=(x+20)/(3)} \\\\ {y=(x)/(3)+(20)/(3)} \\\\ y=0.334x+6.67}\end{array}`

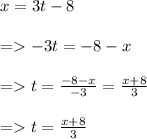
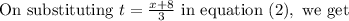
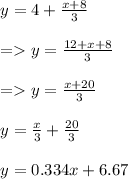
Hence equation
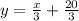`y=(x)/(3)+(20)/(3)` represents variable y in terms of x.