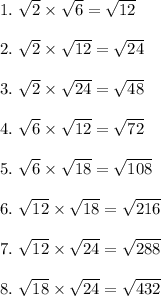Question

Use the list of five irrational below to answer the questions

Square root of 2, Square Root of 6, Square Root of 12, Square Root of 18, and Square Root of 24.
Part A. Choose two numbers whose product is RATIONAL. Explain.
Part B. Choose two numbers whose product is IRRATIONAL. Explain.

Answer 1

`\text{A.}\ √(2)*√(18)\\\\\text{B.}\ √(2)*√(6)`

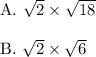
Explanation:

A: The root will be rational if the product of the numbers under the radicals is a perfect square. For this part, there are a couple of choices.

`\text{1.}\ √(2)*√(18)=√(36)=6\\\\\text{2.}\ √(6)*√(24)=√(144)=12`

__

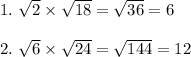
B: The root will be irrational if the product of the numbers under the radicals is not a perfect square. For this part, there are many choices.

`\text{1.}\ √(2)*√(6)=√(12)\\\\\text{2.}\ √(2)*√(12)=√(24)\\\\\text{3.}\ √(2)*√(24)=√(48)\\\\\text{4.}\ √(6)*√(12)=√(72)\\\\\text{5.}\ √(6)*√(18)=√(108)\\\\\text{6.}\ √(12)*√(18)=√(216)\\\\\text{7.}\ √(12)*√(24)=√(288)\\\\\text{8.}\ √(18)*√(24)=√(432)`