Question

Find values of a and b that make the following equality into identity:

x−1/(x+1)(x−4) = a/x+1 + b/x−4

Answer 1

The value of a and b in given expression must be
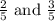`(2)/(5) \text { and } (3)/(5)` respectively so that given equality becomes identity.

Solution:

Need to find the value of a and b in following expression so that following equality will become identity.

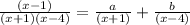`((x-1))/((x+1)(x-4))=(a)/((x+1))+(b)/((x-4))` ------- eqn 1

Lets Simplify Right hand Side first,

`(a)/((x+1))+(b)/((x-4))=(a(x-4)+b(x+1))/((x+1)(x-4))`

`\begin{array}{l}{=(a x-4 a+b x+b)/((x+1)(x-4))} \\\\ {=(a x+b x-4 a+b)/((x+1)(x-4))} \\\\ {=((a+b) x-4 a+b)/((x+1)(x-4))}\end{array}`

`=>(a)/((x+1))+(b)/((x-4))=((a+b) x-4 a+b)/((x+1)(x-4))`

`\text {On substituting } (a)/((x+1))+(b)/((x-4))=((a+b) x-4 a+b)/((x+1)(x-4)) \text { in equation } 1 \text { we get }`

`((x-1))/((x+1)(x-4))=((a+b) x-4 a+b)/((x+1)(x-4))`

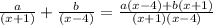
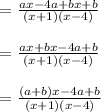
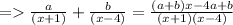
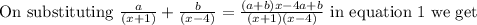
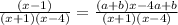
On multiplying both sides by (x+1)(x-4) we get

`((x-1))/((x+1)(x-4)) *(x+1)(x-4)=((a+b) x-4 a+b)/((x+1)(x-4)) *(x+1)(x-4)`

`\Rightarrow x-1=(a+b) x-(4 a-b)`

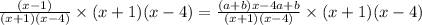
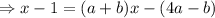
On comparing coefficient of x and constant term separately, we get

a + b = 1 and 4a - b = 1

On adding the two equations we get

a + b + 4a - b = 1 + 1

=> 5a = 2

=>
`a = (2)/(5)`

`\text {Substituting } \mathrm{a}=(2)/(5) \text { in equation } a+b=1, \text { we get }`

`\begin{array}{l}{(2)/(5)+b=1} \\\\ {\Rightarrow b=1-(2)/(5)=(3)/(5)}\end{array}`

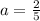
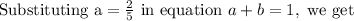
So the value of a and b in given expression must be
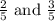`(2)/(5) \text { and } (3)/(5)` so that given equality becomes identity.