Question

Given: <SPT = <RQT, ST = RT Prove: PR = QS​

Answer 1

See explanation

Explanation:

Consider triangles PTS and QTR. In these triangles,

• 
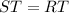  `ST=RT` - given;
• 
  `\angle SPT=\angle RQT` - given;
• 
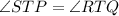  `\angle STP=\angle RTQ` - as vertical angles when lines PR and SQ intersect.

Thus,
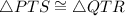`\triangle PTS\cong \triangle QTR` by AAS postulate.

Congruent triangles have congruent corresponding sides, so

`PT=QT`

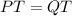
Consider segments PR and QS:

`PR=PT+TR\ [\text{Segment addition postulate}]\\ \\QS=QT+TS\ [\text{Segment addition postulate}]\\ \\PT=QT\ [\text{Proven}]\\ \\ST=RT\ [\text{Given}]`

So,

`PR=SQ\ [\text{Substitution property}]`