Answer: Choice C
RootIndex 12 StartRoot 8 EndRoot Superscript x
12th root of 8^x = (12th root of 8)^x
![\sqrt[12]{8^(x)} = \left(\sqrt[12]{8}\right)^(x)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/zvyyfuz8zef4e8q5pg6qpmq1rrv2fnkve6.png)
=========================================
Step-by-step explanation:
The general rule is
![\sqrt[n]{x} = x^(1/n)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/4pofcy44zsrwq2ubego5i8x2n9necud75j.png)
so any nth root is the same as having a fractional exponent 1/n.
Using that rule we can say the cube root of 8 is equivalent to 8^(1/3)
![\sqrt[3]{8} = 8^(1/3)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/uz4wgpj1afu8schritc991q7l80zsu9cze.png)
-----
Raising this to the power of (1/4)x will have us multiply the exponents of 1/3 and (1/4)x like so
(1/3)*(1/4)x = (1/12)x
In other words,
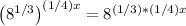
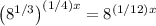
-----
From here, we rewrite the fractional exponent 1/12 as a 12th root. which leads us to this
![8^((1/12)x) = \sqrt[12]{8^(x)}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/tw3053b215spa8r6iyoyp9u7ssk4j6qk4o.png)
![8^((1/12)x) = \left(\sqrt[12]{8}\right)^(x)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/u8us3yjg6h997jj5688n9yyh7ezhsdqb0b.png)