Question

A 60kg block innitially at rest is pulled to the right a long a horizontal force of12N. Find the speed of the block after it has moved 3M if the surface in contact have a coefficient of kinetic friction of 0.15​

Answer 1

The speed of the block after it has moved 3M if the surface in contact have a coefficient of kinetic friction of 0.15​ is 1.7s m/sec

Step-by-step explanation:

Given:

mass of the block = 6.0 kg

Force with which the block is pulled = 12 N

Kinetic friction \mu= 0.15

Distance travelled s = 3 m

To Find:

speed of the block after it has moved 3 metres =?

Solution :

W know that the friction formula is

`f_k = \mu m g`

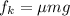
Substituting the values,

`f_k = (0.15)(6)(10)`

`f_k= 9 N`

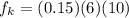
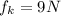
Now Acceleration is Given by

`a=(F -f_k)/(m)`

`a=(12 - 9)/(60)`

`a=(3)/(6)`

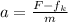
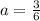
a= 0.5
`m/s^2`

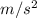
Initial velocity is u = 0

Also we know that,

`v^2 - u^2=2as`

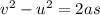
So the equation becomes

`v^2 =2as`

`v=√(2as)`

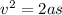
Substituting the values,

`v=√(2as)`

`v=√(2(0.5)(3))`

`v= √(3)`

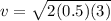
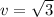
v= 1.73 m/s