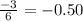Question

What is the sum of the solutions of x2 + 9x + 20 = 0?

What is the product (or multiplication) of the solutions of 6x2 + 7x = 3?

Answer 1

Sum of the solutions of
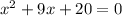`x^2+9x+20=0` is -9.

Product of the solutions of
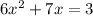`6x^2+7x=3` is
`-0.50`

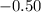
Explanation:

1.
`x^2+9x+20=0`

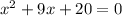
Given:

The expression whose sum of the solution is required is given as:

`x^(2) +9x+20=0`

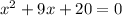
For a quadratic equation of the form
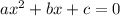`ax^2+bx+c=0` the sum of the solutions is given as:

Sum =
`(-b)/(a)`

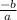
Here,
`a=1,b=9,c=20`

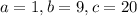
Therefore, the sum of the solutions =
`-(9)/(1)=-9`

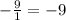
2.
`6x^2+7x=3`

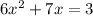
Rewriting the above equation in a standard quadratic equation, we get:

`6x^2+7x-3=0`

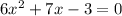
For a quadratic equation of the form
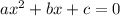`ax^2+bx+c=0` the product of the solutions is given as:

Product =
`(c)/(a)`

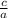
Here,
`a=6,b=7,c=-3`

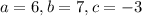
Therefore, the product of the solutions =
`(-3)/(6)=-0.50`