Question

!!!!!!!!!!!!!!!!!!!!​

Answer 1

Option 3

The solution for given expression is
`((x - 4)(x - 4))/((x + 3)(x + 1))`

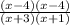
Solution:

Given that we have to divide,

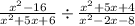`(x^2 -16)/(x^2 + 5x + 6) / (x^2 + 5x + 4)/(x^2 -2x - 8)` ---- (A)

Let us first factorize each term and then solve the sum

Using
`a^2 - b^2 = (a + b)(a - b)`

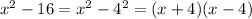`x^2 -1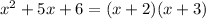6 = x^2 - 4^2 = (x + 4)(x -4)` ----- (1)

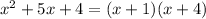`x^2 + 5x + 6 = (x + 2)(x + 3)` ----- (2)

`x^2 + 5x + 4 = (x+1)(x + 4)` ---- (3)

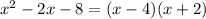`x^2 -2x - 8 = (x-4)(x + 2)` ---- (4)

Now substituting (1), (2), (3), (4) in (A) we get,

`((x + 4)(x -4))/((x +2)(x +3)) / ((x+1)(x+4))/((x-4)(x +2))`

To do division with fractions, we turn the second fraction upside down and change the division symbol to a multiplication symbol at the same time. Then we treat this as a multiplication problem, by multiplying the numerators and the denominators separately.

`((x + 4)(x -4))/((x +2)(x +3)) * ((x - 4)(x + 2))/((x + 1)(x + 4))`

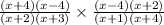
On cancelling terms we get,

`= ((x -4)(x-4))/((x + 3)(x + 1))`

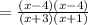
Thus option 3 is correct