Question

A loan of $46,000 is made at 7% interest, compounded annually. After how many years will the amount due reach $65,000 or more?

Answer 1

After 5.11 years, amount due reach $65,000 or more

Solution:

Given that a loan of $46,000 is made.

Rate of interest charged is 7% compounded annually

Need to determine number of years in which the amount due reach $65,000 or more.

In our case

Amount due A = $65000

Loan Amount that is principal P = $46000

Rate of interest r = 7%

Formula for Amount compounded anually is as follows:

`\mathrm{A}=P\left(1+(r)/(100)\right)^(n)`

Substituting the values in above formula we get

`\begin{array}{l}{65000=46000\left(1+(7)/(100)\right)^(n)} \\\\ {(65000)/(46000)=\left((107)/(100)\right)^(n)} \\\\ {\Rightarrow 1.4130=(1.07)^(n)}\end{array}`

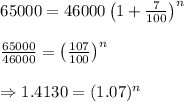
Applying log on both sides, we

`\begin{array}{l}{\ln 1.4130=n \ln 1.07} \\\\ {=>(\ln 1.4130)/(\ln 1.07)=\mathrm{n}} \\\\ {=>\mathrm{n}=(0.34571)/(0.067658)=5.1096=5.11}\end{array}`

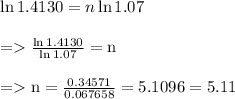
Hence after 5.11 years , amount due reach $65,000 or more