Answer:
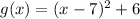
g(x) is a translation of f(x) 7 units to the right and 6 units up.
Explanation:
Let the equation of the function g(x) be
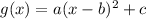
This curve passes through the points (9,10), (5,10) and (7,6), then their coordinates satisfy the equation:
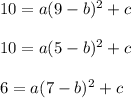
Subtract the second equation from the first:

Then
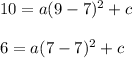
So,

Hence,
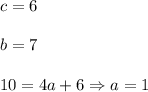
The expression for g(x) is
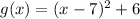
g(x) is a translation of f(x) 7 units to the right and 6 units up.