Final Answer:
The length of NT in isosceles triangle RST is 7.
Step-by-step explanation:
In an isosceles triangle, the base angles are congruent, and the sides opposite those angles are also congruent. Let's denote the length of RS (and RT) as r, and the length of MN as m Since M and N are midpoints, MN is parallel to the base, and its length is half the length of the base. Therefore,
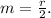
The perimeter of the triangle is the sum of the three sides, so
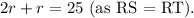 Solving for r, we get
Solving for r, we get
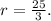
Now, we know that
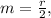 so
so
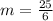 . Finally, the length of NT is the difference between RT and MN, which is
. Finally, the length of NT is the difference between RT and MN, which is
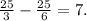 Therefore, the length of NT is 7 units.
Therefore, the length of NT is 7 units.