Answer:
Area of ΔDEF is
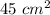 .
.
Explanation:
Given;
ΔABC and ΔDEF is similar and ∠B ≅ ∠E.
Length of AB =
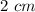 and
and
Length of DE =
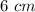
Area of ΔABC =
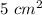
Solution,
Since, ΔABC and ΔDEF is similar and ∠B ≅ ∠E.
Therefore,
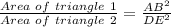
Where triangle 1 and triangle 2 is ΔABC and ΔDEF respectively.
If two triangles are similar, then the ratio of the area of both triangles is proportional to the square of the ratio of their corresponding sides.
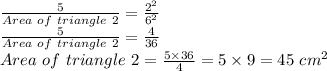
Thus the area of ΔDEF is
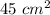 .
.