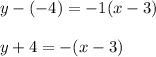Answer:
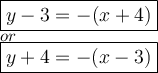
Explanation:
The point-slope form of an equation of a line:
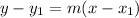
m - slope
(x₁, y₁) - point on a line
The formula of a slope:
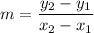
We have two points (-4, 3) and (3, -4).
Substitute:
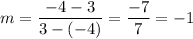
Put the value of a slope and the coordiantes of the point (-4, 3) or (3, -4) to the equation of a line:
for (-4, 3)
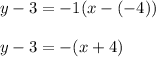
for (3, -4)