Question

There were 346 tickets purchased for a major league baseball game. The lower reserved tickets cost $9.50 and the upper reserved tickets cost $8.00. The total amount

of money spent was $3224.00. How many of each kind of ticket were purchased?​

Answer 1

The total number of lower reserved tickets is 304 and

The total number of upper reserved tickets is 42

Explanation:

Given as :

The total tickets purchased = 346

The price for lower tickets = $ 9.50

The price for upper tickets = $ 8.00

The total amount spent on tickets = $ 3224

Let the number of lower tickets = L

The number of upper tickets = U

Now, According to question

L + U = 346 ........1

And 9.50 L + 8 U = 3224 ....2

so , 8 ( L + U ) = 346 × 8

or, 8 L + 8 U = 2768

And 9.50 L + 8 U = 3224

Now, solving equation

( 9.50 L + 8 U ) - ( 8 L + 8 U ) = 3224 - 2768

Or, 1.50 L + 0 = 456

Or, L =
`(456)/(1.50)`

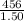
∴ L = 304

Put the value of L in eq 1

So, L + U = 346

I.e U = 346 - L

Or, U = 346 - 304

∴ U = 42

Hence The total number of lower reserved tickets is 304 and

The total number of upper reserved tickets is 42 . Answer