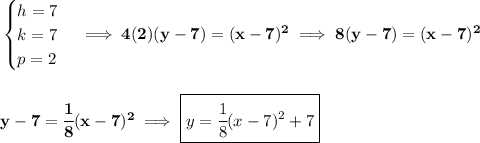Question

A parabolà can be drawn given a focus of (7,9) and a

directrix of y = 5. Write the equation of the parabola
in any form.​

Answer 1

from the provided focus point and directrix, we can see that the focus point is above the directrix, meaning is a vertical parabola and is opening upwards, thus the squared variable will be the "x".

keeping in mind the vertex is half-way between these two fellows, Check the picture below.

`\bf \textit{vertical parabola vertex form with focus point distance} \\\\ 4p(y- k)=(x- h)^2 \qquad \begin{cases} \stackrel{vertex}{(h,k)}\qquad \stackrel{focus~point}{(h,k+p)}\qquad \stackrel{directrix}{y=k-p}\\\\ p=\textit{distance from vertex to }\\ \qquad \textit{ focus or directrix}\\\\ \stackrel{`

`\bf \begin{cases} h = 7\\ k = 7\\ p = 2 \end{cases}\implies 4(2)(y-7)=(x-7)^2\implies 8(y-7)=(x-7)^2 \\\\\\ y-7=\cfrac{1}{8}(x-7)^2\implies \boxed{y=\cfrac{1}{8}(x-7)^2+7}`