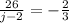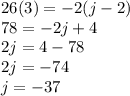Question

A line through the points $(2, -9)$ and $(j, 17)$ is parallel to the line $2x + 3y = 21$. What is the value of $j$?

Answer 1

j=-37

Explanation:

step 1

Find the slope of the given line

we have

`2x+3y=21`

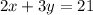
Convert to slope intercept form

Isolate the variable y

subtract 2x both sides

`3y=-2x+21`

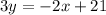
divide by 3 both sides

`y=-(2)/(3)x+7`

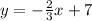
The slope is

`m=-(2)/(3)`

step 2

we have the points

(2,-9) and (j,17)

Find the slope

The formula to calculate the slope between two points is equal to

`m=(y2-y1)/(x2-x1)`

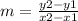
substitute

`m=(17+9)/(j-2)`

`m=(26)/(j-2)`

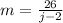
Remember that

If two lines are parallel then their slope are equal

therefore

`(26)/(j-2)=-(2)/(3)`

`26(3)=-2(j-2)\\78=-2j+4\\2j=4-78\\2j=-74\\j=-37`