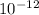Question

An electron confined on one-dimensional infinite potential well has an energy of 180ev. What its wavelength?

Answer 1

The wavelength is 91.5 pm ( 91.5 Pico meter).

Explanation:

The formula can be expressed below for electron’s energy,

`\text {Energy of electron}=(p^(2))/(2 m)`

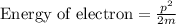
Where,

p = momentum

m= mass of electron

We know, mass of electron =
`9.1 * 10^(-31) \mathrm{kg}`

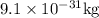
Energy of electron,
`1 e V=1.6 * 10^(-19) \mathrm{J}`

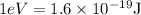
Therefore,
`\text { energy of electron, 180 eV }=180 * 1.6 * 10^(-19) J`

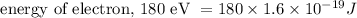
By substituting the known values in the equation, we get,

`180 * 1.6 * 10^(-19)=(p^(2))/(2 * 9.1 * 10^(-31))`

`p^(2)=180 * 1.6 * 10^(-19) * 2 * 9.1 * 10^(-31)`

`p^(2)=5241.6 * 10^(-50)`

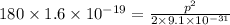
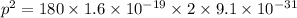
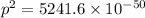
Taking square root, we get

`\text {Momentum, } p=72.399 * 10^(-25) \mathrm{kg} . \mathrm{m} / \mathrm{s}`

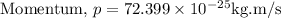
We know,

`\lambda=(h)/(p)`

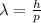
Here, h – Planck constant =
`6.626 * 10^(-34) \mathrm{J.s}`

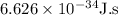
So, the wavelength would be,

`\lambda=(6.626 * 10^(-34))/(72.399 * 10^(-25))=0.0915 * 10^(-34+25)=0.0915 * 10^(-9) \mathrm{m}`

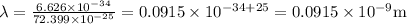
Adding
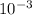`10^(-3)` in both numerator and denominator we get the value as

`\lambda=0.0915 * 10^(-9) * (10^(-3))/(10^(-3))=0.0915 * 10^(3) * 10^(-12)=91.5 \mathrm{pm}`

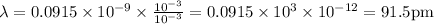
Where, pm – Pico meter -
`10^(-12)`