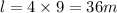The length of the wire is 36 m.
Step-by-step explanation:
Given, Diameter of sphere = 6 cm
We know that, radius can be found by taking the half in the diameter value. So,
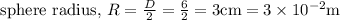
Similarly,
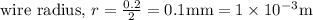
We know the below formulas,
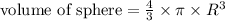
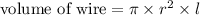
When equating both the equations, we can find length of wire as below, where
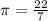
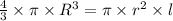
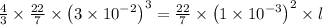
The
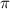 value gets cancelled as common on both sides, we get
value gets cancelled as common on both sides, we get
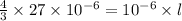
The
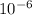 value gets cancelled as common on both sides, we get
value gets cancelled as common on both sides, we get