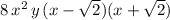Question

Factor the polynomial completely. 8x^4y – 16x^2y^2

Answer 1

8\,x^2\,y\,(x-\sqrt{2} )(x+\sqrt{2} )

Explanation:

Let's start by extracting all common factors from the two terms of this binomial. These common factors are: 8,
`x^2`, and
`y`.

The extraction renders:

`8\,x^2\,y\,(x^2-2)`

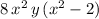
In the real number system, the binomial in parenthesis can still be factored out considering that 2 is the perfect square of
`√(2)`, that is:

`2=(√(2) )^2`

We can then forwards with the factoring of this binomial using the factorization of a difference of squares as:

`(x^2-2) = (x^2-(√(2) )^2)=(x-√(2) )(x+√(2) )`

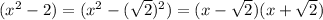
Thus giving the complete factorization as:

`8\,x^2\,y\,(x-√(2) )(x+√(2) )`

Answer 2

8x^4y – 16x^2y^2=

=8x^4y-16x^4y

=-8x^4y

=-8*(x^4y)