Answer:
There are
 rows in the theater.
rows in the theater.
Explanation:
Given terms.
Seats in order
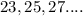 will form an Arithmetic progression.
will form an Arithmetic progression.
As the common difference
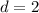 ,same for three consecutive terms so this an AP.
,same for three consecutive terms so this an AP.
Now accordingly we can put the AP terms.
Total number of seats
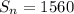
Seats in the first row

Seats in the last row
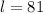
Summation of
 terms in AP
terms in AP
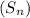
![S_n={(n)/(2)[2a+(n-1)d]}](https://img.qammunity.org/2020/formulas/mathematics/high-school/69prulfgkxek5eh0d0glo0nsf8jnz4zrim.png)
OR
![S_n=(n)/(2)[a+l]](https://img.qammunity.org/2020/formulas/mathematics/college/d7m2v9xiaid5ifbf0742q164lzy5mtcz56.png)
Using the second equation.
![S_n=(n)/(2)[a+l]](https://img.qammunity.org/2020/formulas/mathematics/college/d7m2v9xiaid5ifbf0742q164lzy5mtcz56.png)
![1560=(n)/(2)[23+81]](https://img.qammunity.org/2020/formulas/mathematics/high-school/kdddkpm8ewox0ehptin91mbjjtgexwfjhw.png)
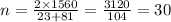
So the number of rows (n) in the theater
