Question

Use Pascal’s Triangle to determine the third term of the expansion of (x + 3)4.

Answer 1

In the Pascal Expansion of
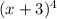`(x+3)^4` the third term is
`54x^2`.

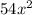Explanation:

Here, the given expression is given as
`(x+3)^4`

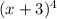
Now, by the PASCAL'S TRIANGLE EXPANSION:

`(a + b)^4 = 1(a)^4 + 4(a)^3b + 6(a)^2b^2 + 4(a)b^3 + 1b^4\\= 1 + 4b + 6a^2 + 4b^3 + b^4.`

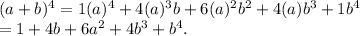
Substituting a = x and b = 3, we get:

`(x + 3)^4 = 1(x)^4 + 4(x)^3(3) + 6(x)^2(3)^2 + 4(x)(3)^3 + 1(3)^4\\= x^4 + 12x^3 + 54x^2  + 108x+ 81`

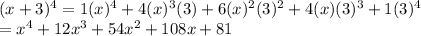
In the given expansion, the third term is
`54x^2`.

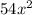Hence, in the Pascal Expansion of
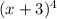`(x+3)^4` the third term is
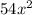`54x^2`.