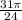Answer:
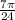 and
and
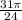
Explanation:
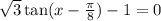
Let's first isolate the trig function.
Add 1 one on both sides:

Divide both sides by
 :
:
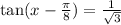
Now recall
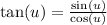 .
.
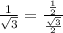
or
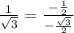
The first ratio I have can be found using
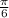 in the first rotation of the unit circle.
in the first rotation of the unit circle.
The second ratio I have can be found using
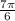 you can see this is on the same line as the
you can see this is on the same line as the
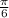 so you could write
so you could write
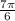 as
as
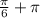 .
.
So this means the following:
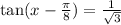
is true when
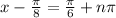
where
 is integer.
is integer.
Integers are the set containing {..,-3,-2,-1,0,1,2,3,...}.
So now we have a linear equation to solve:
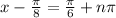
Add
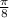 on both sides:
on both sides:
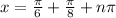
Find common denominator between the first two terms on the right.
That is 24.
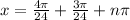
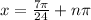 (So this is for all the solutions.)
(So this is for all the solutions.)
Now I just notice that it said find all the solutions in the interval
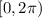 .
.
So if
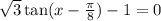 and we let
and we let
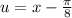 , then solving for
, then solving for
 gives us:
gives us:
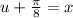 ( I just added
( I just added
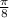 on both sides.)
on both sides.)
So recall
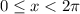 .
.
Then
 .
.
Subtract
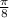 on both sides:
on both sides:

Simplify:
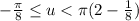
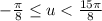
So we want to find solutions to:
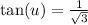 with the condition:
with the condition:
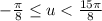
That's just at
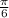 and
and
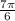
So now adding
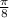 to both gives us the solutions to:
to both gives us the solutions to:
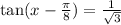 in the interval:
in the interval:
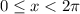 .
.
The solutions we are looking for are:
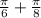 and
and
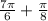
Let's simplifying:
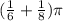 and
and
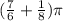
 and
and
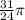
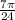 and
and