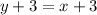Question

Of the following equations below, which equation represents a direct variation between x and y?

Select one:
A. 2y = 3x −7
B. y −4 = x +6
C. y +3 = x +3
D. 4y +1 = 4x−1

Answer 1

C. y +3 = x +3

Explanation:

We need to find in below option x has direct variation with y.

We solve for each;

A.
`2y = 3x-7`

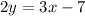
From above equation we can state that 2 times y is equal to 7 less than 3 times of x.

Hence it doesn't represent direct variation.

B.
`y-4 = x+6`

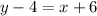
Solving above expression we get;

`y-4 = x+6\\y = x+6+4\\y=x+10`

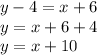
From above equation we can state that y is equal to 10 more than x.

Hence it doesn't represent direct variation.

C.
`y+3 = x+3`

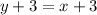
Solving above expression we get;

`y+3 = x+3\\y = x+3-3\\y=x`

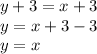
From above equation we can state that y is equal to x.

Hence it represent direct variation.

D.
`4y+1 = 4x-1`

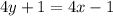
Solving above expression we get;

`4y+1 = 4x-1\\4y = 4x-1-1\\4y=4x-2`

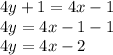
From above equation we can state that 4 times y is equal to 2 less than 4 times of x.

Hence it doesn't represent direct variation.

Hence the Answer which represent direct variation of x and y is,

C.
`y+3 = x+3`