Answer:
Here is the complete question.
Form a polynomial whose zeros and degree are given.
Zeros:-4, multiplicity 1; 3, multiplicity 2; degree 3
Explanation:
Lets decode the question first then we will find the equation of the polynomial.
Here multiplicity are meant for exponents/power to that zeroes preceding before.
Take zeroes of the polynomial then its multiplicity.
When the zeroes are negative then the numbers in the parentheses will be positive or vise versa.Suppose it says
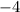 is the zeroes then we will consider it as
is the zeroes then we will consider it as
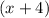 .
.
So consider the zeroes and its multiplicity then repeat it.
We need not to touch the degree part when we re arranged the terms degrees will be part of it,it is just to confirm the answer.
The whole question can be read as:
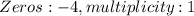 and
and
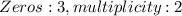
Then
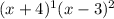
Whenever we expand it by applying algebraic identity it will have degree
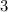 for sure.
for sure.
Now,
 Using
Using


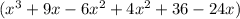
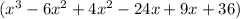

So the final equation of the polynomial is
 .
.