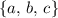Question

Select the relations that are functions.

{(a, 1), (6, 1), (C, 1)}
{(a, a),(a, b),(a, c)}
{(1, a),(2, a),(3, a)
{(a, a),(b, b), (c, c)

Answer 1

Depending on how the input of each function defined,

• The first choice
  `\left\lbrace(a, 1),\, (6, 1), \, (C, 1)\right\rbrace`,
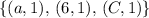• The third choice
  `\left\lbrace(1, a),\, (2, a), \, (3, a)\right\rbrace`
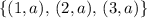
• The fourth choice
  `\left\lbrace(a, a),\, (b, b), \, (c, c)\right\rbrace`

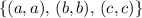
might be functions.

Explanation:

A function between two sets (domain and range) should

• be defined for all elements in the domain, and
• map each element from the domain to exactly one element in the range.

The second choice can't be a function since the element
`a` from the domain is mapped to more than one element in the range.

Keep in mind that a function should be defined for all elements in its domain. For the first relation to be a function, its domain needs to be
`\lbrace a,\, 6, \, C\rbrace`. Similarly, the domain for the third and fourth relations should be
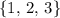`\lbrace 1,\, 2, \, 3\rbrace` and
`\lbrace a,\, b, \, c\rbrace`