Question

You are given the polar curve r = cos(θ) + sin(θ)

a) List all of the points (r,θ) where the tangent line is horizontal. In entering your answer, list the points starting with the smallest value of and limit yourself to (r > or equal to 0) and θ: [0, 2pi] If two or more points share the same value of r, list those starting with the smallest value of θ.

Point 1 (r,θ): ?
Point 2 (r,θ): ?
Point 3 (r,θ): ?

b) repeat this with a tangent vertical line

Answer 1

a) 1.30656∠(3π/8), 0.541196∠(15π/8)

b) 1.30656∠(π/8), 0.541196∠(5π/8)

Explanation:

The critical points can be found in polar coordinates by considering ...

`\displaystyle{dy\over dx}={dy/d\theta\over dx/d\theta}={r\cos\theta + r'\sin\theta\over -r\sin\theta + r'\cos\theta} \quad\text{where $r'=dr/d\theta$}`

We can simplify the effort a little bit by rewriting r as …

`r=√(2)sin((\theta+\pi /4))`

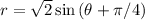
Then, filling in function and derivative values, we have …

`(dy)/(dx)=(√(2)(sin((\theta+\pi /4))cos((\theta))+cos((\theta+\pi /4))sin((\theta))))/(√(2)(-sin((\theta+\pi /4))sin((\theta))+cos((\theta+\pi /4))cos((\theta))))\\\\=(sin((2\theta+\pi /4)))/(cos((2\theta+\pi /4)))\\\\(dy)/(dx)=tan((2\theta +\pi /4))`

__

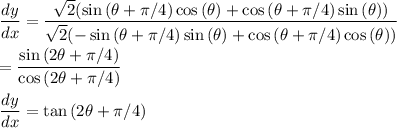
(a) For horizontal tangents, dy/dx = 0, so we have …

`tan((2\theta+\pi /4))=0\\\\2\theta+(\pi)/(4)=k\pi \quad\text{for some integer k}\\\\\theta=k(\pi)/(2)-(\pi)/(8)`

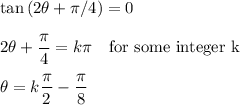
We can use reference angles for the “r” expressions and write the two horizontal tangent point (r, θ) values of interest as …

`(√(2)\sin{(3\pi)/(8)},(3\pi)/(8))\ \text{and}\ (√(2)\sin{(\pi)/(8)},(15\pi)/(8))`

__

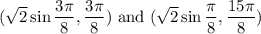
(b) For vertical tangents, dy/dx = undefined, so we have …

`2\theta+(\pi)/(4)=k\pi +(\pi)/(2) \quad\text{for some integer k}\\\\\theta=k(\pi)/(2)+(\pi)/(8)`

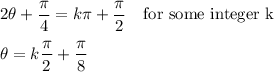
Again using reference angles for “r”, the two vertical tangent point values of interest are …

`(√(2)\sin{(3\pi)/(8)},(\pi)/(8))\ \text{and}\ (√(2)\sin{(\pi)/(8)},(5\pi)/(8))`

__

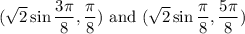
The attached graph shows the angle values in degrees and the radius values as numbers. The points of tangency are mirror images of each other across the line y=x.