Answer:
a=55
b=5
T=17
Explanation:
The general form of the equation is:
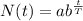
For t = 0:

Since there has been a fivefold increase after 17 years, at t = 17, N(17) = 55*5
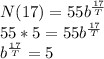
If at every 17*n years there in an increase of 5^n, one can deduct that the values for T and b are respectively 17 and 5:
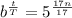
Therefore, the function that represents N(t) is:
