Question

The solution to the given system of linear equations lies in which quadrant?

Ex-3y = 6
1 x+y=2
Quadrant III
Quadrant !
- 5
4
-3 -2
1
2
3
4
5
X
Quadrant III
| Quadrant IV
? 17​

Answer 1

For those who want a quick answer. Its D on edge

Explanation:

Answer 2

The solution to the given systems of linear equation is {3, -1} lies in IV Quadrant.

Explanation:

Given:

x-3y = 6 ........( 1 )

x+y=2 ........( 2 )

To find :

x = ?

y = ?

Solution:

Let solve the above equation to get the solutions.

Eliminate X by subtracting the two equations equation 1 minus equation 2

`(x-3y) - (x+y) = 6 - 2\\-4y = 4\\\therefore y=-1`

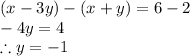
Now substitute for y = -1 in equation 2 we get

`x+(-1)=2\\\therefore x = 2+1\\\therefore x = 3`

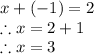
Therefore, solution set is {3, -1}

In

I Quadrant {x,y} = {+,+}......both the coordinates are positive.

II Quadrant {x,y} = {-,+}.....X coordinate is negative and Y coordinate is positive.

III Quadrant {x,y} = {-,-}......both the coordinates are negative.

IV Quadrant {x,y} = {+,-}.....X coordinate is positive and Y coordinate is negative. {3,-1}

Point A on the graph is the solution.