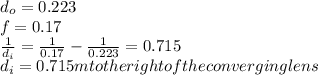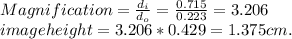Answer:
The object for the converging lens is upright and 0.429 cm tall, the image of this converging lens is inverted and 1.375 cm high
Step-by-step explanation:
Let
![d_(o)=distance of object[tex]\\f=focal length\\d_(i)=distance of image\\I_(h)=Image height](https://img.qammunity.org/2020/formulas/physics/high-school/3pdl6iip9jh3i0auy9lbamydy66zgloqff.png)
For diverging lens:

Magnification =
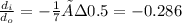
Image height
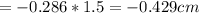 (negative sign means the image is virtual, inverted.
(negative sign means the image is virtual, inverted.
This image is
 meter to left of the center of the diverging lens.
meter to left of the center of the diverging lens.
The converging lens is located 0.08 m to the right of the diverging lens
The distance between the image of the diverging lens and center of the converging lens =
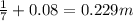
The image of the diverging lens becomes the object of the converging lens.