Question

The Bernoulli equation is valid for steady, inviscid, incompressible flows with a constant acceleration of gravity. Consider flow on a planet where the acceleration of gravity varies with height so that g=g0−cz, where g0 and c are constants. Integrate "F=ma" along a streamline to obtain the equivalent of the Bernoulli equation for this flow.

Answer 1

`p+(1)/(2)ρV^(2)+ρg_(0)z-(1)/(2)ρcz^(2)=constant`

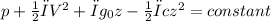
Step-by-step explanation:

first write the newtons second law:

F
`_(s)`=δma
`_(s)`

Applying bernoulli,s equation as follows:

∑
`δp+(1)/(2) ρδV^(2) +δγz=0\\`

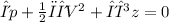
Where,
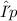`δp` is the pressure change across the streamline and
`V` is the fluid particle velocity

substitute
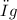`ρg` for {tex]γ[/tex] and
`g_(0)-cz` for
`g`

`dp+d((1)/(2)V^(2)+ρ(g_(0)-cz)dz=0`

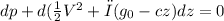
integrating the above equation using limits 1 and 2.

`\int\limits^2_1  \, dp +\int\limits^2_1 {((1)/(2)ρV^(2) )} \, +ρ \int\limits^2_1 {(g_(0)-cz )} \,dz=0\\p_(1)^(2)+(1)/(2)ρ(V^(2))_(1)^(2)+ρg_(0)z_(1)^(2)-ρc((z^(2))/(2))_(1)^(2)=0\\p_(2)-p_(1)+(1)/(2)ρ(V^(2)_(2)-V^(2)_(1))+ρg_(0)(z_(2)-z_(1))-(1)/(2)ρc(z^(2)_(2)-z^(2)_(1))=0\\p+(1)/(2)ρV^(2)+ρg_(0)z-(1)/(2)ρcz^(2)=constant`

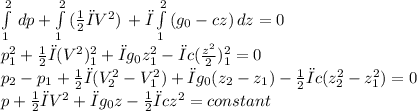
there the bernoulli equation for this flow is
`p+(1)/(2)ρV^(2)+ρg_(0)z-(1)/(2)ρcz^(2)=constant`

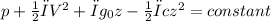
note:
`ρ`=density(ρ) in some parts and change(δ) in other parts of this equation. it just doesn't show up as that in formular