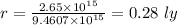Question

The closest stars are 4 light years away from us. How far away must you be from a 854 kHz radio station with power 50.0 kW for there to be only one photon per second per square meter? Assume that the photons spread out spherically. The area of a sphere is 4????????2.

Answer 1

The distance from the radio station is 0.28 light years away.

Solution:

As per the question:

Distance, d = 4 ly

Frequency of the radio station, f = 854 kHz =
`854* 10^(3)\ Hz`

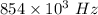
Power, P = 50 kW =
`50* 10^(3)\ W`

`I_(p) = 1\ photon/s/m^(2)`

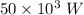
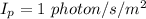
Now,

From the relation:

P = nhf

where

n = no. of photons/second

h = Planck's constant

f = frequency

Now,

`n = (P)/(hf) = (50* 10^(3))/(6.626* 10^(- 34)* 854* 10^(3)) = 8.836* 10^(31)\ photons/s`

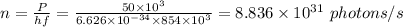
Area of the sphere, A =
`4\pi r^(2)`

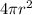
Now,

Suppose the distance from the radio station be 'r' from where the intensity of the photon is
`1\ photon/s/m^(2)`

`I_(p) = (n)/(A) = (n)/(4\pi r^(2))`

`1 = (8.836* 10^(31))/(4\pi r^(2))`

`r = \sqrt{(8.836* 10^(31))/(4\pi)} = 2.65* 10^(15)\ m`

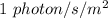
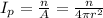
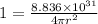
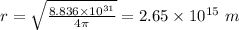
Now,

We know that:

1 ly =
`9.4607* 10^(15)\ m`

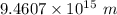
Thus

`r = (2.65* 10^(15))/(9.4607* 10^(15)) = 0.28\ ly`