Question

(a) What is the length of a simple pendulum that oscillates with a period of 3.2 s on Earth, where the acceleration due to gravity is 9.80 m/s2, and on Mars, where the acceleration due to gravity is 3.70 m/s2?

Length (Earth)=?

Length (Mars)=?



(b) What mass would you need to suspend from a spring with a force constant of 20 N/m in order for the mass-spring system to oscillate with a period of 3.2 s on Earth, where the acceleration due to gravity is 9.80 m/s2, and on Mars, where the acceleration due to gravity is 3.70 m/s2?



Mass (Earth)=?

Mass (Mars)=?

Answer 1

Step-by-step explanation:

The expression relating length and time period

T = 2π
`\sqrt{(l)/(g) }`

3.2 =
`2\pi \sqrt{(l)/(9.8) }`

l = 2.54 m

On Mars g = 3.7

`3.2 = 2\pi \sqrt{(L)/(3.7) }`

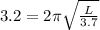
L = .96 m

b )

Expression for elastic constant and time period is as follows

`T  = 2\pi \sqrt{(m)/(k) }`

`3.2=2\pi \sqrt{(m)/(20) }`

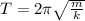
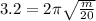
m = 5.19 N/s

Time period of oscillation due to spring is not dependent on g , so same time period will be found on Mars as that on the earth.