Answer:
v > 133.5 m/s
Step-by-step explanation:
Let's analyze this problem a little, park run a complete circle we must know the speed of the system at the top of the circle.
Let's start by using the concepts of energy to find the velocity at the top of the circle
Initial. Top circle
Em₀ = K + U = ½ m v² + m g y
If we place the reference system at the bottom of the cycle y = 2R = L
Em₀ = ½ m v² + m g y
final. Low circle
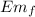 = K = ½ m v₁²
= K = ½ m v₁²
Emo =
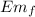
½ m v² + m g y = 1/2 m v₁²
v₁² = v² + (2g L)
v₁² = v² + 2 g L
The smallest value that v can have is zero, with this value the bullet + block system reaches this point and falls, with any other value exceeding it and completing the circle. Let's calculate for this minimum speed point
v₁ = √2g L
We already have the speed system at the bottom we can use the moment
Starting point before crashing
p₀ = m v₀
End point after collision at the bottom of the circle
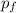 = (m + M) v₁
= (m + M) v₁
The system is formed by the two bodies and therefore the forces to last before the crash are internal and the moment is conserved
p₀ =
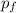
m v₀ = (m + M) v₁
v₀ = (m + M) / m v₁
Let's replace
v₀ = (1+ M / m) √ 2g L
Let's reduce to the SI system
m = 40 g (kg / 1000g) = 0.040 kg
Let's calculate
v₀ = (1 + 1.35 / 0.040) RA (2 9.8 0.753)
v₀ = 34.75 3.8417
v₀ = 133.5 m / s
the velocity must be greater than this value
v > 133.5 m/s