Question

Consider a two-firm oligopoly facing a market inverse demand curve of P = 100 – 2(q1 + q2), where q1 is the output of Firm 1 and q2 is the output of Firm 2. Firm 1's marginal cost is constant at $12, while Firm 2's marginal cost is constant at $20. In Cournot equilibrium, how much output does each firm produce?

1. q1 = 14; q2 = 11
2. q1 = 16; q2 = 12
3. q1 = 18; q2 = 8

Answer 1

option (2) q1 = 16; q2 = 12

Step-by-step explanation:

Given:

P = 100 - 2(q1 + q2)

here,

q1 is the output of Firm 1 and q2 is the output of Firm 2

Firm 1's marginal cost = $12

Firm 2's marginal cost = $20

Now,

Profit maximising level of output is attained where the marginal revenue equals the marginal cost

Thus,

for firm 1,

Total revenue, TR = P×Q

TR = (100 - 2q1 - 2q2) × q1

or

TR = 100q1 - 2(q1)² - 2(q1)(q2)

also,

MR =
`(\delta TR)/(\delta Q)`

thus,

MR = 100 - 4q1 - 2q2

MC = $12

now

MR = MC

or

100 - 4q1 - 2q2 = 12

or

88 = 4q1 + 2q2

or

q2 = 44 - 2q1 ............... (1)

also,

for firm 2, we have

TR = (100 - 2q1 - 2q2) × q2

or

TR = 100q2 - 2(q1)(q2) - 2(q2)²

and,

`MR = (\delta TR)/(\delta Q)`

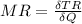
or

MR = 100 - 2q1 - 4q2

and

MC = $20

Now,

MR = MC

or

100 - 2q1 - 4q2 = 20

or

80 - 4q2 = 2q1

or

40 - 2q2 = q1 .....................(2)

Now,

substituting the value of q2 from (1), we get

q1 = 40 - 2(44 - 2q1)

or

q1 = 40 - 88 + 4q1

or

3q1 = 48

or

q1 = 16 units

substituting the value of q1 in equation (1) , we get

q2 = 44 - 2 × 16

or

q2 = 12 units

Therefore,

The correct answer is option (2) q1 = 16; q2 = 12