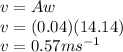Answer:
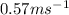
Step-by-step explanation:
k = spring constant of the spring = 40 Nm⁻¹
A = amplitude of the simple harmonic motion = 4 cm = 0.04 m
m = mass of the block attached to spring = 0.20 kg
w = angular frequency of the simple harmonic motion
Angular frequency of the simple harmonic motion is given as

 = Speed of the block as it pass the equilibrium point
= Speed of the block as it pass the equilibrium point
Speed of the block as it pass the equilibrium point is given as