Question

Two speakers separated by a distance of D = 3.90 m emit sound with opposite phase. A person listens from a location d1 = 2.75 m in front of one of the speakers. What is the lowest (nonzero) frequency that gives destructive interference in this case?

Answer 1

Hence lowest (nonzero) frequency that gives destructive interference in this case = 3400 Hz

Step-by-step explanation:

Since, the two are in out of phase,

their path difference is

d= nλ

`d_2-d_1= n\lambda`

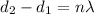
Given d1= 2.75 m

D= 3.90 m

`d_2= √(D^2- d_1^2)`

`d_2= √(3.90^2- 2.75^2)`

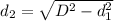
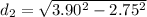
d_2= 2.76 m

2.76-2.75= 1×λ

λ= 0.01 m

0.01= 1*λ

λ =0.01

frequency ν = v/λ = 340/0.01

f= 3400 Hz

Hence lowest (nonzero) frequency that gives destructive interference in this case = 3400 Hz