Question

A beam of x-rays with wavelength λ = 0.300 nm is directed toward a sample in which the x-rays scatter off of electrons that are effectively free. The wavelength of the outgoing electrons is measured as a function of scattering angle, where a scattering angle of 0 means the direction of the x-rays was unchanged when passing through the sample. When looking at all possible scattering angles, what are the longest and shortest wavelengths that the scattered x-rays can have?

Answer 1

Step-by-step explanation:

The problem relates to Compton Effect in which electrons are scattered due to external radiation . The electron is scattered out and photons relating to radiation also undergo scattering at angle θ .

The formula relating to Compton Effect is as follows

`\lambda_f-\lambda_i=(h)/(m_0c) (1-cos\theta)`

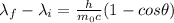
Here
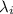`\lambda_i` = 3 0 x 10⁻¹¹

For longest
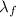`\lambda_f` θ =180°

`\lambda_f` =
`\lambda_i + (2* h)/(m_0c)`

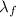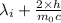
= .3 x 10⁻⁹ +
`(2*6.6* 11^(-34))/(9*10^(-31)*3*10^8)`

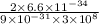
= .348 nm

For shortest wavelength θ = 0

Putting this value in the given formula

`\lambda_f=\lambda_i`

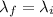
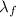`\lambda_f` = .3 nm