Answer:
(a)
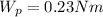
(b)

(c) v= 4.42 m/s
(d) x = 20cm
Step-by-step explanation:
(a) The work done on the block by the gravitational force is:
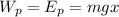
where
 : is the work by the gravitational force,
: is the work by the gravitational force,
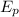 : potential energy, m: is the block's mass, g: gravitational acceleration and x: is the distance of compression
: potential energy, m: is the block's mass, g: gravitational acceleration and x: is the distance of compression
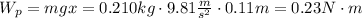
(b) The work done on the block by the spring is given by:
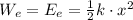
where
 : work by the spring force,
: work by the spring force,
 : potential elastic energy, k: spring constant, x: distance of compression
: potential elastic energy, k: spring constant, x: distance of compression
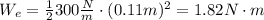
(c) The speed of the block just before it hits the spring can be calculated by conservation of energy before and after the impact:
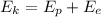
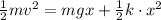 (1)
(1)
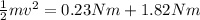
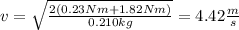
(d) Using equation (1) we can determine the spring compression when the speed at impact is duplicated:

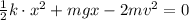 (2)
(2)
Solving the quadratic equation (2), we have the next spring compression (x):
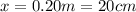
So, an increase in the speed at impact will also increase the spring compression.
I hope it helps you!