Question

A man starts walking north at 4 ft/s from a point P. Five minutes later a woman starts walking south at 5 ft/s from a point 500 ft due east of P. At what rate are the people moving apart 15 minutes after the woman starts walking

Answer 1

Both are moving apart with the rate of 8.99 feet per sec.

Explanation:

From the figure attached,

Man is walking north with the speed = 4 ft per second

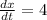`(dx)/(dt)=4` feet per sec.

Woman starts walking due south with the speed = 5ft per second

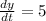`(dy)/(dt)=5` ft per sec.

We have to find the rate of change in distance z.

From the right angle triangle given in the figure,

`z^(2)=(x+y)^(2)+(500)^(2)`

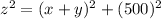
We take the derivative of the given equation with respect to t,

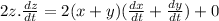`2z.(dz)/(dt)=2(x+y)((dx)/(dt)+(dy)/(dt))+0` -----(1)

Since distance = speed × time

Distance covered by woman in 15 minutes or 900 seconds = 5(900) = 450 ft

y = 4500 ft

As the man has taken 5 minutes more, so distance covered by man in 20 minutes or 1200 sec = 4×1200 = 4800 ft

x = 4800 ft

Since, z² = (500)² + (x + y)²

z² = (500)² + (4500 + 4800)²

z² = 250000 + 86490000

z = √86740000

z = 9313.43 ft

Now we plug in the values in the formula (1)

2(9313.43)
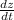`(dz)/(dt)` = 2(4800 + 4500)(4 + 5)

18626.86
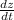`(dz)/(dt)` = 18(9300)

`(dz)/(dt)=(167400)/(18626.86)`

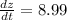`(dz)/(dt)=8.99` feet per sec.

Therefore, both the persons are moving apart by 8.99 feet per sec.