Question

A new gel is being developed to use inside padding and helmets to cushion the body from impacts. The gel is stored in a 4.1 m^3 cylindrical tank with a diameter of 2 m. The tank is pressurized to 1.3 atm of surface pressure to prevent evaporation. A total pressure probe located at the bottom of the tank reads 60 ft of water. What is the specific gravity of the gel contained in the tank?

Answer 1

`SE_(gel) = 3.75`

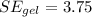
Step-by-step explanation:

First, we have to calculate the gel's column height using the cylinder's volume, as follows:

`V=\pi* r * h\\h=(V)/(\pi * r)\\h=(4.1m^3)/(\pi * 1m)= 1.30 m`

Then, as the pressure given at the bottom of the tank is the sum of the surface pressure and the gel's column pressure, we need to calculate only the gel's column pressure:

ft of water is a unit of pressure, but we need to convert it to atm and then to Pa, in order to calculate our results in the correct units. Therefore, the conversion factor is:

1 ft of water (4°C) = 0.0295 atm

`60 ft water * (0.0295 atm)/(1 ft water)= 1.77  atm\\P_(bottom)=P_(surface)+P_(gel)\\P_(gel)=P_(bottom)-P_(surface)=1.77 atm - 1.3 atm\\P_(gel)= 0.47 atm* (101325Pa)/(1 atm)=47622.75 Pa`

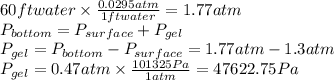
Now, to calculate the specific gravity, we need to find first the gel's density:

`P_(gel) = \rho gh\\\rho = (P_(gel))/(gh)=(47622.75 Pa)/(9.8 m/s^2 * 1.30m)= 3738.04 (kg)/(m^3)`

`SE_(gel) = (\rho_(gel))/(\rho_(water))= (3738.04 kg/m^3)/(997 kg/m^3) = 3.75\\SE_(gel) =3.75`

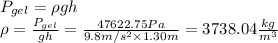
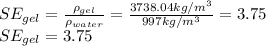
The specific gravity of the gel is 3.75.