Answer:
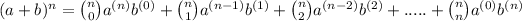
Explanation:
The Given question is INCOMPLETE as the statements are not provided.
Now, let us try and solve the given expression here:
The given expression is:
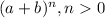
Now, the BINOMIAL EXPANSION is the expansion which describes the algebraic expansion of powers of a binomial.
Here,
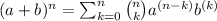
or, on simplification, the terms of the expansion are:
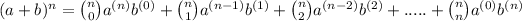
The above statement holds for each n > 0
Hence, the complete expansion for the given expression is given as above.